Click here for this information in PDF format (approx. 35 kilobytes — use it if you want a clean printout)
Ballistics is a subject which is rarely well modelled in a roleplaying system, and for good reason. To accurately reflect the behaviour of a ballistic object in game terms would invariably mean adding needless complications to the rules which would impact severely on playability. Nevertheless, sometimes it's helpful to know a little about the way ballistic objects behave. For example, exactly how far can you throw that Volkswagen down an apartment building corridor without bouncing it off the roof?
In the following graph, trajectories are plotted for an object. The launch energy and object mass in each case is assumed to be identical, but the launch angle is progressively increased. As you can see, maximum range is achieved (as would be expected) with a launch angle of about 40°.
The figures shown in red are the launch angle. The Y-axis shows Loft (the apogee, or maximum height of the trajectory), the X-axis shows Range (the distance the object travels), as a percentage of the total maximum range.
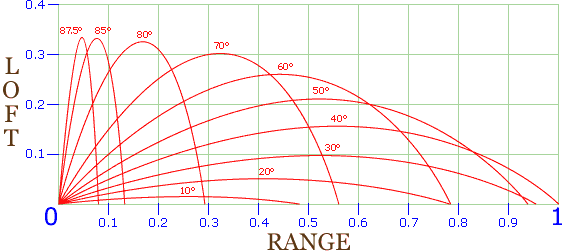 |
| Launch Angle | % of Max. Range | Loft (% of Max. Range) |
|---|
| 10° | 48.2 | 1.5 |
| 20° | 78.2 | 5.1 |
| 30° | 95.5 | 9.7 |
| 40° | 100 | 15.6 |
| 50° | 93.9 | 21.0 |
| 60° | 78.4 | 25.9 |
| 70° | 56.0 | 30.1 |
| 80° | 29.2 | 32.5 |
| 85° | 13.2 | 33.1 |
| 87.5° | 7.9 | 33.3 |
| EXAMPLE: Distance units are measured in terms of a percentage of the maximum possible range. Therefore, if the projectile has a maximum range of 1000 metres, then a launch angle of 70° will send it 560 metres, reaching a height of 301 metres at the top of its trajectory (56% and 30.1%, respectively, of 1000 metres). |
How long does it take?
Good question. It's easy enough to find out how long the projectile will take to fall to earth from apogee (the top of the trajectory), since it falls at gravity's 10m/s/s acceleration. The problem lies in finding out how long it will take to reach apogee.
In vertical firing tests, rifle bullets have been shown to reach an altitude of about 3,000 metres, taking approximately 20 seconds on the way up (being progressively slowed by atmospheric drag and gravity) and 40 seconds down again. If we assume that a projectile will take about half as long to reach apogee as to descend from it, then we can use the Falling Table on p.175 of the 4th Ed. HSR to determine a total flight time. A projectile thrown (or shot) up at a high angle will have a longer flight time than one with a flatter trajectory, even though its total range may be shorter. Note: This is a very inaccurate method of determining actual flight time, but I have no particular desire to delve any further into the arcane mysteries of ballistics than this.
Let's try two examples from the trajectory table above, the first with a launch angle of 30° and the second with 60°, with a maximum possible range of 1000 metres.
The first, launched at 30°, has an apogee of 97 metres and a range of 955 metres. According to the Falling Table, it takes about 3.5 seconds to fall that distance. Add another 1.75 seconds to reach apogee, returns a total flight time of about 5 seconds.
The second example, launched at 60°, has an apogee of 259 metres and a range of 784 metres. The Falling Table says about 7 seconds to fall that far, plus 3.5 seconds to reach apogee, total flight time about ten seconds. Twice as long as the first, although it travelled only 80% of the distance in a straight line.
NOTE: An unpowered projectile reaches apogee at about 60% of its range.
